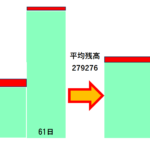
アドオン金利型クレジットの一括返済時の78分法による戻し利息計算を分かり易く説明
目次
78分法の考え方・仕組み
78分法の考え方については「アドオン金利適用クレジットの一括返済時の78分法の導入の経緯」ページの下部で簡単に説明いたしましたが、さらに詳しく説明いたします。
78分法の名前の由来
そもそも78分法と称される所以は、返済を一年の月払い(12回払)で支払った場合、元金は1/12づつ減少していきます。1/12をⅠ枡とした場合、契約時が12桝、次月返済後が11桝、次が10桝と減少していきます。同様に元金残高に比例する手数料(利息)も同じように減少すると考えます。ここで、桝の総和が12+11+10・・・2+1=78になることから”78分法”と呼ばれています。
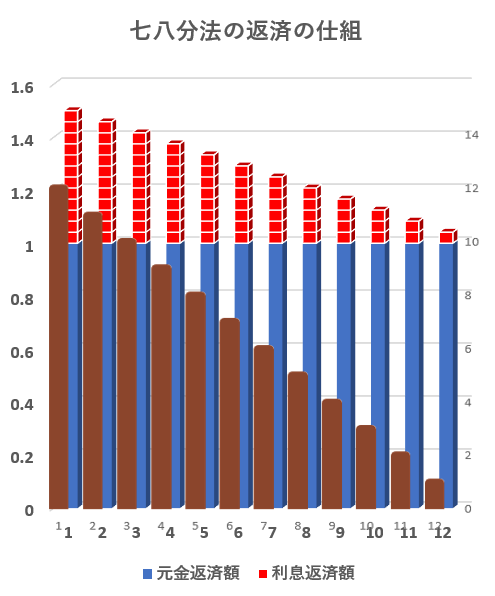
右の図は12回で支払う場合の、元金残高、元金返済金額及び手数料返済額の変化を表にしたものです。
■色の部分は、元金の推移、
■色の部分は、毎月元金返済額
■色の部分は、手数料の毎月返済額
をそれぞれ表しています。
ここで、■色の手数料返済額は、■色の元金残高に比例しています。そして、■色の元金残高の規則正しい階段状の減少幅は、■色の定額の元金返済額を反映したものです。
78分法による戻し手数料を求める計算式
78分法の説明のために12回払いを例に説明いたしましたが、あらゆる回数に適用出来る公式があります。ここで78分法の戻しの計算式を 等差数列 から求め、その応用を試みてみましょう。
手数料の桝目の数は支払回数に応じて次のようになります。
支払回数が1回の場合 =1
支払回数が2回の場合 =1+2
支払回数が3回の場合 =1+2+3
支払回数が4回の場合 =1+2+3+4
・
・
・
支払回数がN回の場合 =1+2+3+4+・・・・+(N-1)+N
回数N回の場合の枡目の数はどのようにして求めることが出来るでしょうか?
Nが偶数の場合を例に求めてみます。
1 + 2 + 3 +4 + 5・・・・・・・・・・(N-3) + (N-2) + (N-1) + N
の両端を足してみます。
つまり
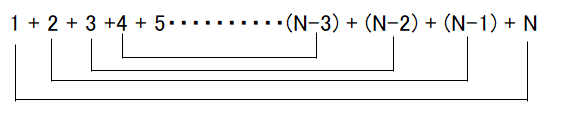
そうすると
(1+N) + (2+(N-1)) + (3+(N-2)) + (4+(N-3)) + ・・・・
=(N+1) + (N+1) +(N+1) + (N+1) + ・・・・
そして、(N+1)が何個あるかといえば、Nの半分、つまりN/2個です
そこで求める総数は、
=N(N+1)/2の計算式で求められます。
Nが奇数の場合も計算式は同じになります。
いま全体の和を求めましたが、今度は未到来の桝目の数を求めます。未到来の回数をnとすれば、計算式は上述と同じになります。
つまり、=n(n+1)/2となります。
それでは、戻し手数料はどうしたら求められるでしょうか?
戻しの部分は、全体の中の未到来の部分です。
つまり、(未到来の個数)/(全体の個数)に手数料をかけて求めることが出来ます。
数式としては、総支払回数=N、未経過支払回数=nとすると
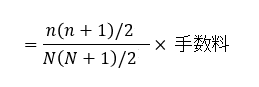
で、分子と分母にそれぞれ2を掛けると
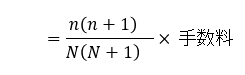 ・・・・・・・①
・・・・・・・①
と纏めることが出来ます。
なお、総支払回数=N、支払経過回数=nとすると
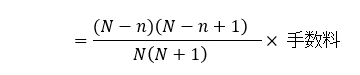 ・・・②
・・・②
に式を変換することも出来ます。
①式は残りの回数が何回かを基に計算し、②式は支払が何回過ぎたかを基に計算しています。
実際は、上記戻し手数料からクレジット会社の一括返済手数料として1~3割を徴求することが有りますので、1割として計算すると以下の通りとなります。
n=未経過回数の場合
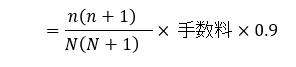
n=経過支払回数の場合
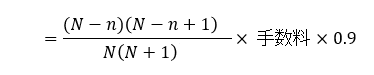
返済月毎の手数料を求める計算式
次に応用例として、毎回の手数料を12回払いを例に求めてみます。
1回目が12個
2回目が11個
3回目が10個
・
・
・
12回目が1個
になっています。
つまり、
1回目(1ヶ月目)は 支払回数に相当
2回目(2ヶ月目)は 支払回数-1に相当
3回目(3ヶ月目)は 支払回数-2に相当
・
・
・
していますので、これを総回数N回の場合の何ヶ月目(経過月数)に相当するかという式に当てはめてみます。
計算式は、総回数+1-何ヶ月目
ここで、総回数=N 経過月数=n とすると
=N+1-n
それでは、経過月の手数料はいくらになるか計算します
全体の和に対する経過月の割合に手数料を乗じれば求められますから
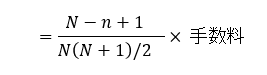
式を変換すると
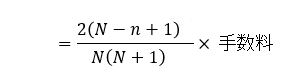
となります。
経過手数料を求める計算式
最後に、戻し手数料がわかれば経過手数料もわかります。
既に戻し手数料がわかっているわけですから、計算式は
総回数=N
経過月数=n
とした場合、(nを未経過月数としない)の経過手数料は、
=(1-(N-n)(N-n+1)/N(N+1))×手数料
貸金における78分法の活用方法
現在ではほとんどありませんが、貸金でもアドオン金利で貸付する場合があります。アドオン金利で貸付けた場合で早期完済が有った場合は月割りで利息を計算して減額するだけでは約定利率を大きく超えた貸付になることがあります。場合によっては、法定の制限利率を上回る可能性もあります。
そのため、戻し利息を計算する場合は日割りで計算する必要が有ります。
日割りの計算式は次の様になります。
翌月以降の戻し利息+早期完済の翌日から早期完済月の月末までの利息
=翌月以降の戻し利息+早期完済月の利息÷30×早期完済日の翌日から月末までの日数
ここで
- 1ヶ月の日数は30日に限定せず実日数で計算
- 早期完済日の翌日から月末までにの日数は、「約定返済日の前日までの日数」
に置換えられる場合があります。
順を追って計算してみます。
まず、翌月以降の戻し利息を求めますが、数式としては、総支払回数=N、未経過支払回数=nとすると
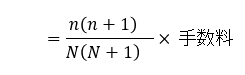 です。
です。
なお、総支払回数=N、支払経過回数=nとすると
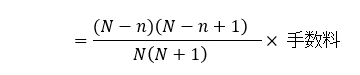
となります。
次に早期完済月の未経過利息を計算しますが、計算式は単月の利息を求め日割り計算します。
総回数=N 経過月数=n とすると
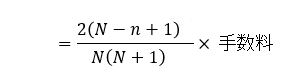
・・・①
となります。
ここで、早期完済月の未経過の利息を計算します。
但し、総回数=N、経過月数=n、利息総額=R、早期完済月の日数=D及び早期完済日の翌日から次回約定日(又は月末)までの日数
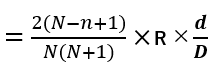
・・・・・・②
上記①及び②の二つの計算式で求められた利息の合計が戻し利息の総額となります。